Probability
1. Introduction
The Probability of Evolution
One of the most common types of anti-evolution argument is the probability-based argument, and its greatest strength is the fact that the average person does not know the concept of probability very well, if at all. Creationists have many creative ways of using public ignorance of probability to their advantage, but the most common trick is to attack abiogenesis: the process by which it is believed that the first self-replicating molecule was produced in the primeval seas, billions of years ago.
Creationist arguments tend to rely on a common misconception: to use a poker analogy, they assume that if you come up with a very good hand, then you must be cheating. "But isn't that true" you might ask? If someone comes up with a very good hand in poker, doesn't that mean he cheated? Not necessarily. It's possible, but you would need better evidence than that.
In order to understand the flaws in the creationist probability argument, one must first understand how you compute probabilities. This should not be above the level of the average person because they teach the basic concepts of probability in high-school algebra class (or at least they did back when I went to school; I don't know if the weakening of educational standards has rotted away this part of the curriculum yet). The basic concept is disarmingly simple: if the process is random, then you simply count the total number of possibilities and then divide it by the number of outcomes you're looking for. The execution, however, can be quite complex and involves many potential pitfalls.
In the following pages, we will examine the concepts of probability with several everyday examples, before looking at an example of a typical creationist probability-based argument where we can put these concepts to use.
2. Examples of Random Probability
When it comes to audience familiarity, the best examples of random probability can be found in the world of gambling. Therefore, two excellent examples are the lottery, and the game of 5-card poker. Warning: ahoy, there be mathematics here! If you hated math in school, you might have trouble getting through this page. If you think you won't be able to handle it, feel free to run like a coward to Page 3, but be aware that by skipping this page, you are proving that you don't have what it takes to discuss probability at even the most basic level. Keep that in mind if you're a creationist and you intend to write me an E-mail telling me how wrong I am.
The Lottery
Lottery games are random (by law), so they are obviously a good example of random probability. Let's take an example lottery where you must pick 6 unique numbers in any order from 1 to 49. Remember that the first step is to count the number of possible combinations: there are 49 choices for the first number. You can't pick the same number twice, so there are only 48 choices for the second number, 47 choices for the third number, and so on. Therefore, the total number of possible combinations is 49*48*47*46*45*44 (or 49!/43! on your calculator), which equals approximately 10.07 billion. However, you can pick the 6 numbers in any order, and there are 720 possible ways to arrange 6 numbers (6*5*4*3*2*1, or 6! on your calculator; now you know what that x! button is for). Therefore, the overall probability is 10.07 billion divided by 720 orders, or 13.98 million (probability math short-hand for this whole process is "49 choose 6", or 49C6). Therefore, the odds of any given set of numbers coming up in this type of lottery are roughly 1 in 14 million. And if you play two sets of numbers in the same lottery draw, then your odds of winning are roughly 2 in 14 million, or 1 in 7 million.
Note: an important recurring formula in probability is
"x choose y", and it looks like this:
x choose y = x!/(x-y)!/y!
This formula, also expressed as xCy (eg- 49C6) will be used
henceforth in lieu of bulky expressions such as
(49*48*47*46*45)/(6*4*3*2*1). The exclamation mark stands for
"factorial". Fun Fact: if you enter "49
choose 6" in Google Search, it will automatically compute the
result for you. Try it!
It must be noted that your odds of winning the lottery do not go up if you have been playing every week for the last 10 years. Did you notice that in the above calculation, no mention whatsoever was made of previous plays? That is because previous plays do not factor into the probability equation at all. If your intuition tells you that your 10 years of prior play should count for something, remember that if one is to learn about scientific and mathematical concepts, one must first learn to listen to the equations, not your intuition. Your intuition is the sum total of your life experience up to now, and it is a very unreliable guide when learning about new and unfamiliar things.
So now you know how to calculate the odds of drawing a particular number in a lottery. Here's an exercise: if you understood the preceding, then calculate the odds of any given set of numbers coming up in a lottery where you pick 4 numbers from 1 to 39. But in this lottery, the order of the numbers does matter, and you can pick the same number more than once. Click here for the answer.
Poker
In the game of poker, you have 52 cards: 4 suits (clubs, spades, hearts, and diamonds), with 13 cards (ranked from ace to king, although ace can be either low or high) in each suit (no jokers or other wildcards for now). Remember that the first step is to calculate the number of possible combinations. You can't draw the same card twice, and the order doesn't matter, so if you draw a 5-card hand from a deck of 52 cards, then the math is similar to the first lottery example: "52 choose 5" = 52C5 = 2598960.
In order to determine the probability of drawing any particular hand out of those 2598960 possibilities, you must determine how many different examples of that hand exist. For example, a royal flush is the five highest cards in any given suit, from ten to ace, like this example:



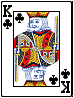

Click on the cards to see all 4 royal flushes: one for each suit. Since there are 4 royal flushes, the odds of a royal flush are 4 in 2598960, or 1 in 649740. Another way of calculating the odds is 20/52*51C4.
For a trickier example, the odds of getting a triple (three of the same number) can be computed by determining how many triples exist in the deck. A triple, also known as "three of a kind", is three cards of the same rank, like this:


 |
 |
 |
Click on any card to see all the combinations available. There are 13 possible ranks of triple, from ace to king, and for each rank, there are 4 ways to get a triple out of the four available suits. Therefore, there are 13*4=52 possible triples. But we still have to pick the last two cards, don't we? Remember that there are 52 cards, we've already used up 3, and the 4th card of the same rank is off-limits because we don't want four of a kind, so so there are 48 cards left to choose from for our 1st unknown. For our 2nd unknown, we don't want a card of the same rank as the 1st unknown because that would be a full house (a triple and a double), so that means there are only 44 cards left to choose from. Therefore, there are 48*44 ways to pick our two unknowns which can be arranged in two orders (1-2 and 2-1), so the total number of combinations is 48*44/2, or 1056. Therefore, there are 52*1056=54912 different possible hands containing triples, so your odds of a triple are 54912 out of 2598960, or approximately 1 in 47.
So now you have an idea of how to calculate poker odds. It's trickier than lottery odds, because when you work with poker odds, the total number of possibilities is just the beginning. Here's an exercise: if you understood the preceding, calculate the odds of drawing a full house. That's a triple and a double, and if you paid attention when we solved the triple, the answer should be easy. Click here for the answer.
If you're feeling confident, you can try two more exercises: first, determine the odds of a straight flush. That's five cards in sequential order, all from the same suit. The lowest card can be an ace (aces can be low or high) but it cannot be a 10, because that would make it a royal flush. Click here for the answer. For a more difficult challenge, try to determine the odds of getting a straight flush if you add two jokers to the deck, and make them both wildcards (a wildcard can be used to fill in for any other card, thus increasing the likelihood of getting a rare hand). Click here for the answer.
So what did we learn?
Hopefully, we learned how simple probability looks at first, but we also learned how tricky it can get. Think of how easily one could go astray when trying to calculate the odds of a triple. If we forgot that the last two cards could be in any order, we would have forgotten to divide by 2!, and our odds would be off by 100%.
3. A Series of Unfortunate Unlikely Events
So far, we've only looked at single events: a single lottery draw or a single hand of poker. What about a series of events? A common creationist tactic is to take a long list of events, assume that they had to occur simultaneously, and then declare that the odds against such an occurrence are astronomically high. This is a quote from a typical creationist argument:
"Proteins are functional because the amino acids are arranged in a specific sequence, not just a random arrangement of left-handed amino acids. The formation of functional proteins at random could be likened to a monkey trying to type a page of Shakespeare using the 26 letters of the alphabet. Anyone knows that the monkey is not capable of accomplishing the task set before him."
That's a pretty impressive argument, right? It's been estimated that it would take longer than the age of the entire universe for a monkey to actually type a page of Shakespeare. But this argument contains a hidden assumption: that the entire page has to be typed at once, or that the entire amino acid sequence has to be assembled at once. What if you can build it piece by piece? What if our hypothetical monkey is allowed to keep typing letters until they assemble a word in the sequence, and then goes on to the next word? Does that change the odds?
As it turns out, it changes the odds tremendously. In order to illustrate this, let's go back to the world of gambling and look at a familiar object: dice. Now I know what you're thinking: you're thinking "This guy has an obsession with gambling. Maybe he should seek help." But leaving my personality flaws aside, let's consider the problem of rolling dice. Specifically, rolling 10 sixes. If you took ten dice in your hand and rolled them, how likely are you to get ten sixes? That's a pretty simple calculation: there are 6^10 possible combinations, so your odds are 1 in 60466176. Of course, you can always try it yourself. The following JavaScript widget will roll dice for you until you get ten sixes:










Did you try it? How long did you wait? At 2 rolls per second and more than sixty million combinations (since the widget keeps the dice in order), you might get lucky in roughly ... one year. Assuming you don't want to wait that long, hit the "Stop" button and try this new widget, which does the same thing but does it one die at a time instead of trying to get them all at once:










That didn't take too long at all, did it? So what was the difference? The difference is that when you have a series of events, there is really no need to assume they all happen simultaneously. You can take them one at a time, adding on sequentially. And when you do so, the odds collapse to relatively tiny numbers because you no longer multiply them together: instead, you add them one at a time, as they happen. So your odds of getting the first six are 1 in 6: something that should take only a few seconds. Then your odds of getting the next six are also 1 in 6, which should also take only a few seconds. On average, you're probably looking at around 30 seconds to get all ten sixes, as compared to a year the other way.
So what did we learn?
When you consider the huge difference between treating sequential events as a series as opposed to a single simultaneous event, you begin to realize just how easily creationists can exaggerate the unlikelihood of series events in evolution, even if we assume that these events are completely random.
Now consider the famous "monkeys typing Shakespeare" argument. If we modified our little die-rolling widget to roll for letters and select good letters, what effect do you think that would have on the time required to reach the goal? Perhaps our monkey should start practising his typing.
Acknowledgements
- The forum user "IPeregrine", for content suggestions.
- Rob Dalton and forum users "Darth Holbytlan" and "Starglider", for debugging assistance.
4. Non-Random Probability
In the previous two pages, we've looked at poker, the lottery, and rolls of the dice: all games of chance. But what if we're looking at a non-random game? It may be possible to derive probabilities, but you would need to know the nature of the non-random mechanism.
Baseball
For example, let's look at a baseball player trying to hit a ball. This is a decidedly non-random situation; if the ball is moving through the middle of the stroke zone, the player reacts to it well, and swings his bat at the ideal time and in the ideal place, the probability of hitting the ball is 100%. Or, if the ballplayer completely misreads the pitch and swings at the wrong time in the wrong place, the probability of hitting the ball is 0%. This is why you cannot generate a reliable prediction for any given ballplayer in any given at-bat; in order to know the probability of him hitting the ball, you need to know factors which cannot be evaluated until after the fact.
"Ah, but we have batting averages" one might answer. That is true; baseball fans have long compiled lists of batting averages which indicate a player's past performance. Baseball statisticians even break them down into specific situations (batting against left-handed pitchers, batting against right-handed pitchers, batting against this particular pitcher, etc). But you still cannot generate a meaningful statistical prediction for any given at-bat, because there are too many variables you cannot evaluate. At best, you can look at past performance and assume that future performance will match, even though you know that many variables will change from year to year, game to game, or even at-bat to at-bat.
Could it be possible to get highly reliable predictions from baseball statistics? One would have to say yes ... if the game were played by robots. The field of statistical probability is not necessarily unreliable or unscientific, but it requires a high degree of experimental control which is just not possible with human beings playing baseball. If you could produce baseball players who were far more consistent in their behaviour (like robots), a more reliable set of statistical probabilities could emerge. However, that's not much of a solution for baseball, unless we switch to robot players. Barry Bonds is a good start in that direction, but the total elimination of the human factor is still many years away.
This is all rather disappointing compared to our nice clean mathematical analyses of poker games and lottery tickets, but unfortunately, that is the nature of reality. The mechanism of poker games and lottery tickets is incredibly simple: random selection from a precisely defined set. However, the mechanisms of real events tend to be considerably more complex. If you could nail down all of the variables and ensure that they remain fixed (impossible in the case of baseball games, but possible to within a high degree of accuracy for scientific experiments), you could use past performance to predict future performance, but the clean mathematical technique is extremely difficult to apply, if not impossible.
A Calculated Non-Random Probability
So is it ever possible to evaluate a non-random probability? Yes, but you need to know a fair bit about the mechanism. When the meteorologists say there is a 70% chance of precipitation, they are saying this based on highly detailed air movements and temperatures, in conjunction with a large body of research into weather patterns and a superb understanding of the mechanism of precipitation. But there are other situations where you can generate reliable probability estimates for non-random (or more accurately, partially random) situations.
Note: at this point, those of you who are starting to feel tired of the mathematics should probably skip ahead to the next page, because we're about to do some more work with poker and dice, and those of you who easily suffer "math fatigue" will probably start tuning out, if I didn't lose you already back on Page 2.
Poker ... again.
Still here? OK, let's manufacture an example of a non-random probability which can be evaluated: suppose you are playing a modified game of poker where you are required to discard any card which is the same rank as a card you are already holding (for example, if you draw a two of spades and a two of clubs, you have to discard the two of clubs and pick up another card). Given this rule, the probability of drawing a double, triple, four of a kind, two pair, or a full house would suddenly drop to precisely zero. But the odds of drawing other hands such as straight flushes would go up, due to a reduced number of alternatives.
For example, let's take the royal flush: there are still just 4 possible royal flushes, but the total number of combinations has changed because so many hands have been outlawed. You could calculate the number of doubles, triples, quadruples, two-pairs, and full houses and then subtract them all from 2598960, but that would be a lot of work. Luckily, there's a much easier way to calculate the odds of a royal flush with our modified rules. You start with the ten card, of which there are 4 in the deck out of 52 cards, or 1 in 13. To get the matching jack, you have to pick 1 of 48 remaining cards (remember that 1 card has already been drawn and the 3 other ten cards are off-limits, so you've got 52-1-3 cards left). In similar fashion, you have to pick 1 of 44 cards to get the matching queen, 1 of 40 cards for the king, and 1 of 36 cards for the ace. And finally, you have to divide by 5!=120 orders. Therefore, the odds are 13*48*44*40*36/120, or 1 in 329472.
Loaded dice.
Another type of non-random probability is the weighted probability. This is still "random", but unevenly so. The classic example of weighted probability is drawn from gambling (yes, gambling again), and it's known by the popular name "loaded dice". Suppose you had dice which had a small metal weight inside, making them three times more likely to land a six than any other number. You could still calculate odds, but if you assumed that the dice were normal, your predictions would not match the results.
The simplest way to account for weighted probabilities is to "double-count". For example, if sixes are 3 times more likely than any other number, you simply assume there are 3 sixes in the dice. So instead of each number having a 1 in 6 probability of coming up, numbers one through five would have a 1 in 8 chance of coming up, and the number six would have a 3 in 8 chance of coming up.
So what did we learn?
Hopefully, we learned that it's very difficult to generate non-random probability estimates unless you know precisely how the non-random mechanism works. Let's say that in our poker example, we knew that there were some special rules for the draw but we didn't know what those rules were. It would become impossible to determine the odds of drawing any particular hand. Worse yet, suppose we didn't even know how many cards were in the deck. Probability estimating is an extremely complicated business, where the smallest unjustified assumption can produce numbers which are completely wrong and where missing information can make any kind of estimate impossible.
5. Summary
OK, let's review. We have learned three things here:
- It is fairly easy to calculate probabilities for a very simple and completely random mechanism, like playing the lottery. However, as we saw in our poker examples, it can get much trickier when you introduce more complexity.
- If you require a series of unlikely events, there is an enormous difference in probability if you treat them as a single simultaneous event instead of treating them as separate events, as demonstrated with the example of rolling dice.
- As we saw in our modified poker example, the instant you introduce as much as a single draw rule of any kind, the draw mechanism becomes non-random. Once the mechanism becomes non-random, any probability calculation based on pure randomness will become useless.
Keep all of those facts in mind when examining any creationist probability argument, because they almost always ignore all of them. In fact, now that you are armed with a basic comprehension of the difficulties inherent in probability calculation, you should be able to see through the following common creationist tricks:
Oversimplification
Creationist probability calculations are usually characterized by their extreme simplicity, as if there's really nothing more to probability than counting the numbers of entities involved in a process and turning them into an exponential figure, with no regard whatsoever for whether the process is characterized by many valid picks or only one. For example, in poker, the odds of drawing a royal flush are very low, but the odds of drawing a double are very high, because there are so many doubles. When creationists speak of the odds of evolution or abiogenesis, how do they know they are looking for a royal flush or a double? How do they know how many valid outcomes exist? Quite tellingly, they never even mention this question, because it's so much easier to assume that there is only one.
They also ignore the question of whether events in a series should be treated as separate events or a single combined event. And yet, as we saw in our "rolling dice" example, this is an enormously important factor. If 500 binary events are required for something, a typical creationist would literally assume that you can compute the odds of this event by simply punching "2^500" into a calculator, with no regard whatsoever for the underlying mechanisms or the manner in which these events should be combined.
The Assumption of Randomness
We have already seen that there is a huge difference between random probabilities and non-random probabilities. Unfortunately, most creationists falsely assume that all natural processes are random, which is why they usually describe evolution as "random chance". And yet, we saw with the case of modified poker that the addition of as little as one rule can completely falsify random probability calculations! If this is the case, then how much effect do all the myriad rules of organic chemistry have? How can anyone seriously call organic chemical reactions "random chance" when they have so many rules that most people struggle to grasp the few rules they describe in high-school chemistry?
The assumption of randomness is so deeply buried into creationist thought that almost no creationists even state it as an assumption; they simply incorporate it silently into all of their arguments and hope that you won't even think to ask the question.
The Missing Information Problem
Once we realize that we are dealing with non-random processes, we run into a serious problem: as we saw in our modified poker example, it would be impossible to calculate the odds of drawing a royal flush if you don't account for the modified draw rule, and it is impossible to account for the modified draw rule if you don't know what it is. In a situation like this, you cannot compute probabilities no matter how much of a skilled mathematician you are.
Now that you (hopefully) understand how difficult it is to generate probability estimates even for a situation where you know most of the variables and mechanisms, how can you generate such precise estimates for events where you don't know so many of the variables? And why does the math behind these creationist probability estimates look so nice and clean and simple?
Are your suspicions raised yet? They should be. You've seen how complicated a probability analysis can be for something as simple as a game of poker. How can creationists possibly derive such mathematically simple probability estimates for something as remarkable as the origins and development of biological life? Sure, you could say that their stratospherically high probability estimates are perfectly reasonable for something you find so alien, but that's not much of an answer, is it? Probability estimates are most accurate when you know the situation very well, not when you don't know it at all. The sheer simplicity of their work is proof of its inaccuracy: the idea that complex catalyzed organic chemical reactions could be modeled in such a manner that they are far simpler than a mere poker game is the height of absurdity, yet it is widely accepted practice in the creationist world.
6. An Example of a Creationist Probability Argument
Now that we've seen how creationists typically operate, it's time to examine the phenomenon "in the wild", so to speak. A good example of a creationist probability argument can be found here . Here is an excerpt:
"In experiments attempting to synthesize amino acids, the products have been a mixture of right-handed and left-handed amino acids. (Amino acids, as well as other organic compounds, can exist in two forms which have the same chemical composition but are three-dimensional mirror images of each other; thus termed right and left-handed amino acids).
One would think that the formation of amino acids into protein would randomly use both left and right-handed amino acids and result in approximately 50 percent use of each. However, every protein in a living cell is composed entirely of left-handed amino acids, even though the right-handed isomer can react in the same way. Thus, if both right and left-handed amino acids are synthesized in this primitive organic soup, we are faced with the question of how life has used only the left-handed amino acids for proteins.
We can represent this dilemma by picturing a huge container filled with millions of white (left-handed amino acids) and black (right-handed amino acids) jelly beans. What would be the probability of a blind-folded person randomly picking out 410 white jelly beans (representing the average sized protein) and no black jelly beans? The odds that the first 410 jelly beans would be all one color are one in 2410."
Can you see how the creationist employs exactly the tricks we could have predicted? The formation of amino acids in living organisms is obviously non-random; why else would we consistently produce only left-handed ones in our bodies? Almost immediately, we see that he has confused a clearly non-random process for a purely random one: a trick he attempts to gloss over by noting that a totally different method for producing amino acids is more random (this is known as the "red-herring" fallacy).
"Ah", a creationist might retort, "but what about the very first amino acids? According to evolutionist beliefs, they weren't produced by living organisms!". That would be correct, but of course, it hides yet another baseless assumption on his part: that the very first amino acids were all left-handed. How could he possibly know that? He admits himself that left-handed and right-handed amino acids are functionally identical, so there's no reason they had to be. His only reason for this assumption is the fact that amino acids formed in living organisms today are all left-handed, and as already noted, that is obviously not a random process.
Here's another excerpt:
"Proteins are functional because the amino acids are arranged in a specific sequence, not just a random arrangement of left-handed amino acids. The formation of functional proteins at random could be likened to a monkey trying to type a page of Shakespeare using the 26 letters of the alphabet. Anyone knows that the monkey is not capable of accomplishing the task set before him.
What is the probability of synthesizing a protein with a specific sequence? Let us simplify the situation first. For example, if there are 17 students in a class, how many possible ways exist for them to order themselves in a line? It would take the students a long time to physically try all the possibilities since there are over 355 trillion different ways. If the number of students were increased to 20, equal to the number of amino acids that exist, the number of possible ways would be over 1018 different ways, the number of seconds in 4.5 billion years!
Remember: this is a simple example of a specific arrangement of 20 amino acids. The probability is even greater when we consider that there are 20 possibilities for each spot. Also, in a specific protein of 100 amino acids, or in the formation of a hemoglobin molecule which has 574 amino acids arranged in a specific sequence, the probability becomes astronomical!
If only one amino acid is changed in the sixth position, the disease sickle cell anemia results. The RNA within the tobacco mosaic virus contains about 6,000 nucleotides. The probability that this molecule resulted by the random chance arrangement of the four nucleotides is 1 out of 46000 or 2.3x103216!"
As one can see from this passage, creationists are almost entirely too predictable. This is really nothing more than the exact same deception he employed in the previous excerpt: assuming that organic chemistry has no rules and is completely random, even though we know that this is false. If you are observant, you may also notice that he assumes without explanation that the small number of amino acids we use are the only kind of amino acids that could possibly work, hence assuming that we're looking for the equivalent of a royal flush in poker. But how does he know the other combinations wouldn't work?
They wouldn't work in our environment because an organism needs to be compatible with the other organisms around it, but how does he know that in an alien environment, an entirely different set of compounds could not have arisen? In other words, how does he know we're looking for a royal flush instead of a triple, which is much more common? The short answer is that he doesn't; like the rest of his argument, it's nothing more than an assumption on his part, used in order to produce an inflated probability figure by heavily oversimplifying a complex situation.
Here is another excerpt:
"Life is not contained within a single protein, however. Several proteins are required for even the basic functions of the simplest living organism. Even the most simple known cell, such as the mycoplasma, may have 750 proteins. The list of proteins essential for survival may be narrowed down to 238 proteins. The probability of forming these 239 proteins from left-handed amino acids has been calculated to be 1 in 1029,345.
It is perhaps telling that he does not divulge the method by which he computed this figure, because it is almost comically absurd. He starts with the false 2410 figure from earlier, and he multiplies it by itself, 238 times. In short, not only does he falsely assume that amino acid formation in living organisms is totally random, but he assumes that every protein must have been created simultaneously, like rolling 238 dice all at once instead of rolling them one at a time. There comes a point where one must seriously question whether a creationist argument is the result of incompetence or deliberate deception, and this argument is fast approaching that point.
Are you starting to see how creationists abuse the concept of probability? Notice how they set you up by treating modern life and ancient life as if they are interchangeable (making assumptions about the most primitive early life forms based on modern life forms, even though the simplest bacteria is still the result of billions of years of evolution), and then they generate preposterously large numbers by deceptively combining many events into one and falsely assuming that organic chemistry has no rules and is therefore totally random. Also notice how incredibly simple their calculations always are; they make our poker analyses seem like highly advanced mathematics by comparison. So why don't you try examining the following excerpt for yourself, to see if you can spot the tricks and oversimplifications?
Many times we hear evolutionists using the term "primitive cell," although we have no example of such. One of the simplest living systems, the tiny bacterial cell, is exceedingly complex. Dr. Michael Denton describes the bacterial cell, which weighs less than 10-12 grams, as: "... in effect a veritable micro-miniaturized factory containing thousands of exquisitely designed pieces of intricate molecular machinery, made up of one thousand million atoms, far more complicated than any machine built by man and absolutely without parallel in the non-living world."
Our human body has over 200,000 types of proteins in its cells, and the odds of just one of those proteins evolving by chance is vast. Sir Fred Hoyle, still an evolutionist, likens this to a blindfolded subject trying to solve the Rubik's cube. The blindfolded man has no way of knowing whether he is getting closer to the solution or actually farther away. According to Hoyle, if the blindfolded subject were to make one random move every second, it would take him on the average three hundred times the supposed age of the earth, 1.35 trillion years, to solve the cube.
Out of the 200,000 proteins in our body, roughly 2,000 provided the very essential function of cellular metabolism, similar to that in a bacterial cell. The odds of those essential enzymes arriving by chance is extremely large, almost improbable. As stated by Drs. Hoyle and Wickramasinghe, "the trouble is that there are about two thousand enzymes, and the chance of obtaining them all in a random trial is only one part in (1020)2000 = 1040,000, which is an outrageously small probability that could not be faced even if the whole universe consisted of organic soup." This is about the same chance as throwing an uninterrupted sequence of 50,000 sixes with a pair of dice.
Rather amusingly, he actually uses the example of rolling dice in his argument: the exact same example we used earlier (complete with a working demonstration) in order to show why this kind of reasoning is incorrect.
So what did we see?
After perusing these kinds of arguments, it becomes quite clear that the creationist is utterly reliant upon the assumption that organic chemistry has no rules and is therefore completely random, even though this assumption is quite obviously false and essentially renders the entire argument invalid. It is also clear that creationists refuse to envision ancient life as being significantly different from modern life, which is why they always assume that the very first life form must have been something like a modern E Coli bacteria rather than a primitive self-replicating molecule. And finally, it is clear that the average creationist either does not know how to perform a probability analysis or is deliberately deceiving his audience.
Return to main Probability page
Jump to:

